From Physics to AI Safety: Cross-Disciplinary Questions for Transformer Interpretability
A two-week deep dive into transformer architecture: a learning journey from fundamentals to physics-inspired research questions.
📖 Reading Time: Executive Summary (2 min) | Full Document (25-30 min)
Executive Summary
This document presents a systematic exploration of transformer architecture through the lens of physics training, building foundational knowledge necessary for mechanistic interpretability research while demonstrating how cross-disciplinary approaches can accelerate understanding of complex AI systems. This work illustrates how domain expertise from physics can provide complementary perspectives on AI safety challenges, with research directions identified that could contribute to advancing interpretability methods, understanding scaling phenomena, and developing more rigorous approaches to analyzing AI systems.
Key Contributions
- Cross-Disciplinary Architecture Understanding: Applied frameworks from physics, biology, and machine learning to understand transformer mechanics, revealing analogies that clarify complex mechanisms like residual streams, positional embeddings, and attention patterns.
- Systematic Learning Methodology: Designed and documented a transferable 6-step process for efficiently acquiring expertise across technical domains—valuable for researchers transitioning into AI safety from other fields.
- Physics-Inspired Research Directions: Identified potential research avenues including group theory applications to neural circuit classification, statistical mechanics approaches to many-body neural systems, and exploring the intersection between scaling laws and phase transitions—questions that may offer fresh methodological angles for interpretability research.
- Technical Implementation: Systematically worked through transformer implementations with hands-on exploration of attention mechanisms, testing different inputs and modifications to build deep understanding of architectural components.
1. Why: Motivation for This Deep Dive
The Pull: Why AI Interpretability Matters
I've always enjoyed learning broadly and deeply—from podcasts and audiobooks spanning big history, brain science, and philosophy to technical tutorials and online courses—driven mostly by curiosity and genuine enjoyment. This habit of connecting insights across seemingly unrelated domains has shaped how I approach complex problems: looking for patterns that emerge when viewing challenges through multiple disciplinary lenses. But this goes beyond personal curiosity—I also believe learning isn't optional; it's directly related to our collective survival. The COVID pandemic illustrated this perfectly: without mRNA vaccine technology—built on decades of accumulated scientific knowledge across multiple fields—humanity could have faced an existential threat.
At the same time, the rapidly exploding pace of new knowledge made me realize I need to learn more efficiently to keep up, while also finding more effective approaches to learning how to learn. Additionally, recently experiencing the loss of loved ones and witnessing devastating events so close to home reinforced that time is our scarcest resource.
These convergent realizations created a dilemma: I can learn forever and find joy in it, but what's the point if I don't use it for something meaningful? This led me to reflect deeply on what problems I feel strongly enough about to be worth my limited time, and how to balance leveraging my existing knowledge with efficiently adopting new tools to tackle challenges that matter.
The answer traces back to questions that have fascinated me since watching "Ghost in the Shell" in the 90s: What makes a human human? My early conclusion was "memory"—and after learning more about brain science, I'm convinced this intuition was correct. Memory is fundamental to emotion, action, identity, and consciousness. Recent films like "After Yang" have renewed these questions about the boundary between human and AI.
With AI systems becoming increasingly sophisticated, I see interpretability research as the perfect intersection of my physics training, my industry experience, and my long-standing fascination with consciousness. Understanding how these systems actually work—reverse-engineering their "memory" and decision-making—feels like the most meaningful problem I can contribute to. I also believe that understanding current AI is a prerequisite for safely developing artificial superintelligence (ASI). It combines the rigor of physics with the profound questions about intelligence that have captivated me for decades, while addressing what I see as a critical foundation for humanity's AI future.
This Project: Learning Experiment
This project also served as an experiment in applying recent insights from brain science to my learning approach. I'd learned that our brains work differently from muscles—the key isn't avoiding fatigue but leveraging how creativity emerges from the default mode network through novel combinations of existing knowledge. I wanted to challenge my traditional "deep focus for a few hours" approach, which I considered my core strength and was often praised for, and become more flexible with planning, revising scope on the fly rather than spending days perfecting initial plans.
Planning: Two-Week Timeline & Scope
With upcoming travel scheduled in four weeks, I saw an opportunity to test whether interpretability research was the right direction for my career transition. Drawing from my previous ultra learning experience, I allocated two weeks for deep exploration, one week for writing, and kept the final week as contingency—a more realistic timeline than my perfectionist tendencies usually allow.
The biggest challenge was that the scope would entirely depend on how efficiently I could learn the fundamentals. Based on early conversations with friends familiar with the field, I pivoted from attempting meaningful analysis using existing methods to focusing on building a solid foundational understanding. I reduced the scope to what I could learn effectively and to the unique perspectives or questions I might contribute through a physicist’s lens. This means I intentionally left out existing interpretability research, which I plan to revisit in future work.
2. How: My Learning Methodology
Prior Knowledge Baseline
Neural Networks Foundation
I already had basic knowledge of neural networks from my academic time - at the very core, they are inspired by our brain, and their power comes from "activation" functions of neurons, which introduce non-linearity and allow the network to learn complex patterns rather than just linear combinations. I also knew that "deep" means the number of layers is larger, which allows better pattern recognition.
Sequential Models Intuition
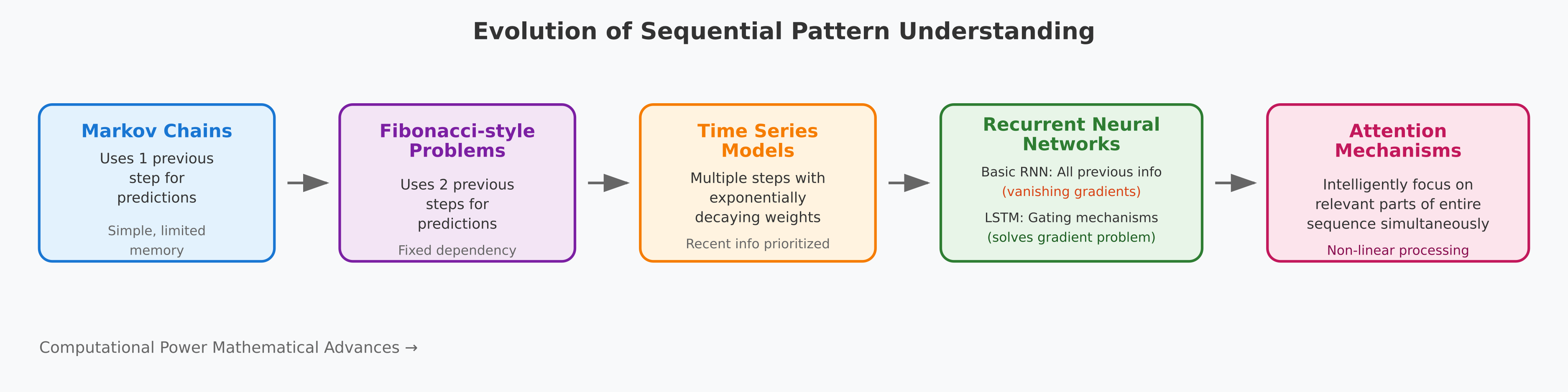
With my physicist mindset, I had this picture in mind: progressively building up the dimensions of information from previous steps. Markov chains utilize one previous step to make predictions, Fibonacci-style problems utilize two previous steps, and time series models utilize multiple previous steps with exponentially decaying weights, focusing more on recent information. RNNs represent the next evolution where we can theoretically use all previous information in a sequence, but they suffer from vanishing gradients over long distances. LSTMs solved this through sophisticated gating mechanisms that can selectively remember and forget information across long sequences. Attention mechanisms represent the latest breakthrough where I don't have to process information linearly—I can intelligently focus on the most relevant parts of the entire sequence simultaneously, making optimal use of multiple previous steps. All of these advances were only possible with the development of powerful computers, allowing many complex operations within much shorter times (similar to how Bayesian inference became practical due to better computing power). Like almost any technological evolution, this represents repeated attempts to solve the same fundamental problem—understanding sequential patterns—by addressing the limitations of previous methodologies with advancing computational capabilities.
Previous Transformer Exposure
I also skimmed through the "Attention is All You Need" paper years ago and understood that it essentially removed the need for RNNs in many sequence modeling tasks. More recently, I also took Andrew Ng's Coursera courses to have a better understanding of both neural networks and deep learning fundamentals as well as generative AI with language models. These were also to gain hands-on implementation experience and build basic knowledge of the necessary tools.
Practical Experience
I led the development of P-Rex, a personalized recommendation system using XGBoost at CloudTrucks, which gave me hands-on experience with feature engineering and production ML deployment. Later, I built an LSTM-based forecasting model, providing exposure to PyTorch and neural network implementation. My work with PostgreSQL and recommendation systems for search ranking also familiarized me with query-key-value concepts used for attention mechanisms in Transformers, though I hadn't worked directly with Transformer architectures previously.
Learning Strategy: Fundamentals Over Trends
Feeling a strong urgency to understand how AI systems actually work, I discovered Anthropic's Mechanical Interpretability Research Scientist job posting and was immediately drawn to their approach of reverse-engineering neural networks. I wanted to quickly assess whether this was the research direction I should pursue, so I dove into the extensive resources provided in their job posting guidelines.
However, after initially trying to follow all available sources sequentially, I became overwhelmed. I started pondering whether I needed to explore the most recent research to stay "current" or return to fully understanding fundamentals. Stepping back, I realized that if my ultimate goal was to understand how AI works through reverse-engineering transformers, it made no sense to skip understanding transformers from scratch. This reminded me of spending considerable time on harmonic oscillators in Classical Mechanics and hydrogen atoms in Quantum Mechanics—fundamentals are essential building blocks.
Building on that, it's simply impossible to "stay current" in depth without solid basics, and this approach aligned with my physics background and natural preference for understanding foundational principles first. I made a conscious decision to prioritize foundational understanding over keeping up with the latest papers, viewing this as both a reality check on my capacity and a strategic choice that matched my learning style.
Finally, I wanted to preserve my "novice" perspective—those fresh questions and potential challenges to existing assumptions that are valuable precisely because of their outsider viewpoint. I knew this perspective would inevitably disappear as I became more familiar with the field, so I made sure to log these initial insights while they were still genuine. Beginner's perspectives can sometimes reveal overlooked assumptions or alternative approaches that experts might miss, but only if captured before that fresh lens is lost to familiarity.
Systematic Learning Approach
My approach to learning something fundamentally new—especially at the cutting edge—relies on structuring the experience to both accelerate early understanding and build deep intuition over time. I've refined this process through years of transitioning between disciplines, and for this deep dive, I leaned heavily on strategies rooted in physics training, modular thinking, brain science insights, and industry experience with rapid iteration cycles. I also specifically sought effective learning resources, and I've distilled this into a repeatable six-step process:
1. Learn terminology & connect to existing knowledge
Memorize new concepts with clear definitions to create basic building blocks—I then only need to figure out hierarchical relationships among them. This follows the Rumpelstiltskin principle: you can't truly understand what you can't name. I also noticed that as I accumulate knowledge across fields, I increasingly spot similar concepts used in different domains.
2. Map hierarchical structure
In books or papers, this is equivalent to understanding the table of contents. This is where I personally benefit most from LLMs. When deciding whether to read a paper, I ask: 1) summarize the whole paper in a few bullet points, 2) what are the strengths and weaknesses, and 3) how would you improve it? I learned this framework from Tae-woong Park's YouTube videos and initially applied it by manually prompting various LLMs. However, as AI tools evolve rapidly, I've since streamlined this process—I now delegate these questions directly to NotebookLM, which has become my default tool for this type of analysis.
3. Skim fast, focus on gaps
This is based on the fact that I already have accumulated fundamental knowledge from other work (basic math, science concepts, etc.). To be efficient about learning new things, I can skim through everything at high speed, then focus on parts I don't understand, get stuck on, or find insightful. This approach was inspired by insights from Dr. Moon-ho Park's YouTube review [1] of The Talent Code [2].
4. Test with hands-on coding
This is empirical validation—understanding output with different inputs builds real understanding and shows how I can materialize/execute ideas.
5. Create visual summaries
From my academic experience, I learned that eventually any research result is summarized as either a figure or a table. Diagrams are visual aids I often use to communicate complicated concepts with team members when presenting projects.
6. Test through active recall
The real test is whether I can explain each concept clearly—this is the critical part of turning memory into knowledge. Writing is often a good way to do this, and this blog also serves this purpose.
Example: This work
A detailed walkthrough of applying this methodology is provided in the Appendix.
3. What: A Cross-Disciplinary Understanding of Transformers
Transformer Architecture Deep Dive
In this section, we focus on a decoder-only transformer, specifically using the same architecture and parameters as GPT-2 Small [3].
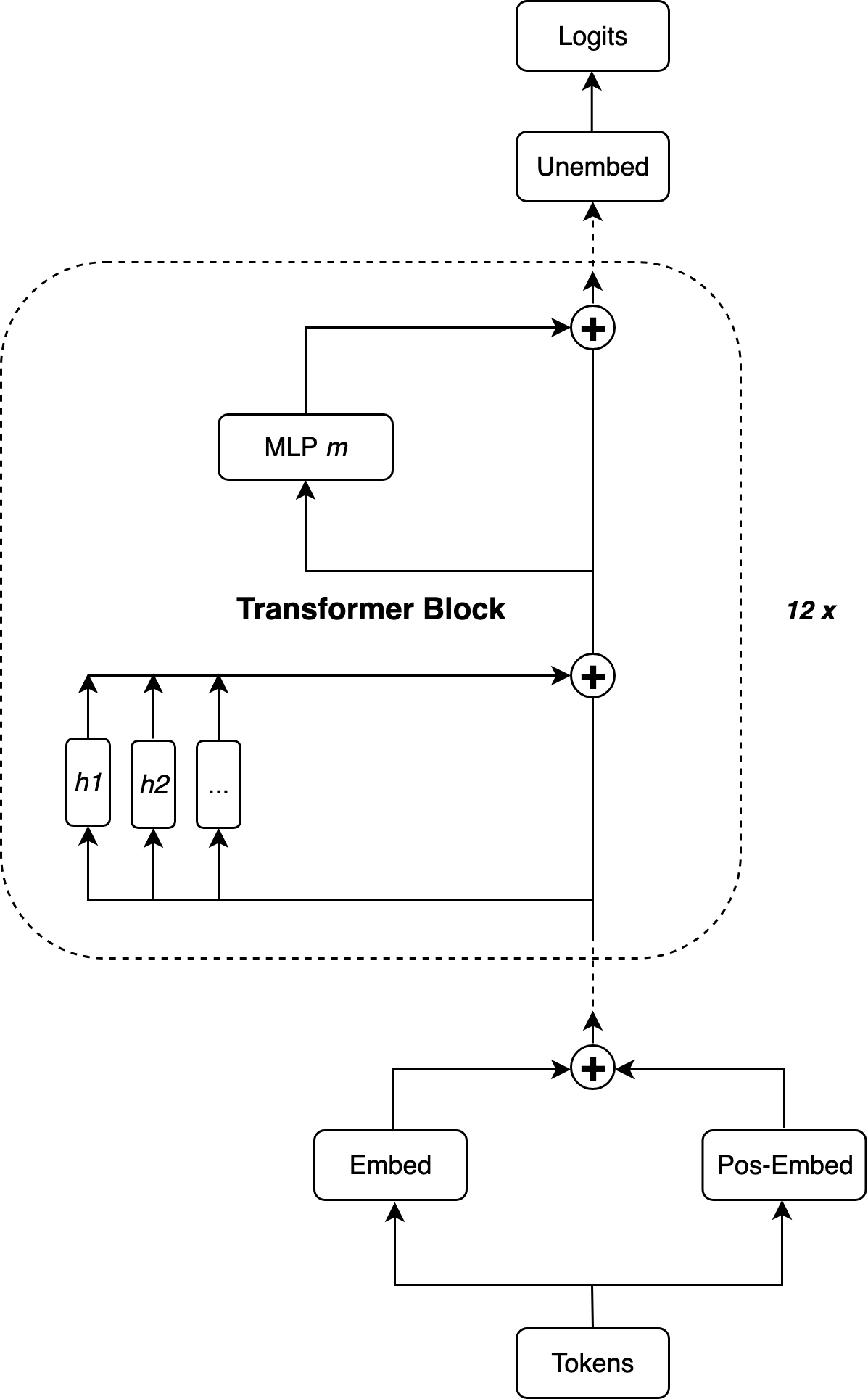
Foundational Concepts
The Residual Stream: Information Highway
At the heart of the transformer lies the residual stream - the main information highway that carries data through each layer. Unlike traditional neural networks where information gets completely transformed at each step, transformers add modifications to this stream while preserving the original information. This is analogous to how we might annotate a document by adding notes in the margins rather than rewriting the entire text. From a physics perspective, this is similar to perturbation theory - we start with an unperturbed state (the original embeddings) and add small corrections at each layer, with each transformer block acting like a perturbative correction that modifies but doesn't replace the underlying state.
Layer Normalization: Preventing Gradient Problems
Layer normalization's primary purpose is maintaining stable gradient flow during training. In deep networks, activations can have wildly different scales across layers, causing gradients during backpropagation to become very small (vanishing) or very large (exploding). Layer normalization solves this by normalizing the activations going into each layer, keeping their scale consistent.
The process: subtract the mean to center at zero, divide by standard deviation to normalize variance, then apply learned scaling and translation parameters. This ensures more stable gradient magnitudes throughout the network during training, allowing the model to learn effectively. The learned scaling (γ) and translation (β) parameters then allow each layer to recover the optimal scale and shift for its specific function, while maintaining the gradient flow benefits.
This creates more stable optimization dynamics, similar to how physicists normalize variables in numerical simulations to prevent computational instabilities when dealing with vastly different scales.
The Transformer Flow
See Fig.2 above starting from bottom to top.1. Tokens: From Text to Integers
Everything starts with converting human-readable text into integers through tokenization. This uses a method called Byte-Pair Encoding - we start with individual characters and iteratively merge the most common pairs. The result is a vocabulary of ~50,000 sub-word tokens that can represent any text. Each token gets mapped to a unique integer ID, which serves as an efficient key for the embedding lookup table.
2. Embedding: From Integers to Vectors
The embedding layer is essentially a giant lookup table that converts each token ID into a high-dimensional vector (768 dimensions in GPT-2). This learned mapping allows the model to represent semantic relationships - similar tokens end up with similar embedding vectors through training.
3. Positional Embeddings: Adding Sequence Information
Since attention is content-based rather than position-based, we need to explicitly tell the model where each token sits in the sequence. We learn another lookup table that maps position indices to vectors, then add these to the token embeddings. The key insight that initially confused me: how does adding positional embeddings to token embeddings not create collisions? The answer lies in the high dimensionality - with embedding vectors of length 768, the probability of collision becomes vanishingly small. This is similar to how CRISPR achieved precision in gene editing: while earlier techniques used shorter recognition sequences (higher collision risk), CRISPR uses ~20-nucleotide guide sequences, making the probability of accidentally matching the wrong genomic location negligibly small.
4. Attention Mechanism: Intelligent Information Routing
This is where the magic happens. For each token, the model computes three vectors: Query (what am I looking for?), Key (what do I contain?), and Value (what information should I pass along?). The similarity between Query and Key vectors determines how much attention each token pays to every other token in the sequence. (During implementation, I discovered that the order of performing Einstein summation operations within each dot product doesn't affect the results—in retrospect it makes total sense because of commutativity and associativity, but it was a little fun moment.)
**Note: In decoder-only transformers like GPT-2, this is specifically self-attention - each token attends to other tokens within the same sequence. This differs from encoder-decoder architectures (like the original Transformer) which also include cross-attention, where decoder tokens attend to encoder representations. Since we have no separate encoder, all attention is self-attention.**
Multi-Head Attention: Rather than having one attention mechanism, transformers use multiple "heads" (12 in GPT-2) that attend to different types of information simultaneously. Each head can specialize - one might focus on syntactic relationships, another on semantic meaning. It's like having multiple experts each contributing their specialized perspective.
Causal Attention: In GPT-style models, we use what's called "causal attention" - though I find this term somewhat misleading from a physicist's perspective. While there's a notion of sequence, there's no true temporal causality. Instead, it's a masking mechanism that prevents tokens from seeing later tokens in sequence, maintaining the sequential prediction task. This is analogous to preventing data leakage in ML (where future information accidentally gets into training features) or blinding in experimental physics (where researchers are kept unaware of group assignments to prevent bias). All three techniques share the same core principle: controlling information flow to maintain the integrity of the process.
The Complete Attention Process: The mechanism follows six precise steps: (1) compute Query, Key, and Value vectors by applying learned linear transformations to the input embeddings, (2) calculate raw attention scores by computing dot products between each Query and every Key vector, (3) scale these scores to prevent extremely large values, (4) apply the causal mask to set future positions to negative infinity (preventing information leakage), (5) convert masked scores to probabilities using softmax, and (6) compute the weighted sum of Value vectors using these probabilities, then apply a final linear transformation to produce the output that gets added back to the residual stream.
5. MLP Layer: Pattern Recognition and Computation
Despite the confusing name "multi-layer perceptron," these are actually simple two-layer feed-forward networks: expand the dimensionality (768 → 3072), apply non-linearity (GELU activation), then contract back (3072 → 768). The expansion (768 → 3072) creates finer granularity by providing more "working space" for complex transformations. The GELU non-linearity then selectively activates different pathways, creating pattern recognition. The contraction (3072 → 768) distills all this rich intermediate computation back into the residual stream format, essentially summarizing the complex high-dimensional processing into a form that can be added back to the information highway.
6. Transformer Blocks: The Core Architecture
The transformer block is the fundamental building unit, consisting of two key steps that always work together in a specific order:
1. Attention Mechanism: Routes and gathers relevant information from across the sequence (Communication Phase)
2. MLP Layer: Processes and transforms this contextualized information (Computation Phase)
This order is crucial: attention first allows each position to collect relevant context from the entire sequence, then the MLP can do informed processing with this enriched representation. The alternative (MLP → Attention) would force the MLP to process information blindly at each position before sharing, like trying to analyze the word "bank" without knowing whether the context involves rivers or money. By putting attention first, we follow the principle of "gather information, then process it" rather than "process locally, then share." This makes computation more effective - the MLP gets to do its complex reasoning on contextualized, relevant information rather than wasting computational effort processing isolated local information that may lack important context.
Each step is preceded by layer normalization (a standard preprocessing necessity before feeding information to any layer, including the final unembed step). Both the attention and MLP outputs are added back to the residual stream via residual connections.
This transformer block pattern repeats 12 times in GPT-2, with each iteration building increasingly complex representations from the combination of attention-driven information gathering and MLP-driven computation.
7. Unembed: Converting to Vocabulary Scores
The final step converts the high-dimensional representations into raw scores over the vocabulary. This is conceptually the reverse of embedding - we apply a linear transformation (matrix multiplication plus bias) from the model dimension (768) to vocabulary size (~50,000), creating one logit score for each possible token type in the vocabulary.
8. Logits: Raw Predictions
These raw scores (shown at the top of Fig. 2) represent the model's unprocessed predictions. During inference, they are converted to probabilities using softmax (not shown in Fig. 2 as it's a mathematical operation, not an architectural component), giving us probability estimates for each possible next token. For token generation, we can sample from this distribution or take the highest probability token. These probabilities also serve as the primary metric for measuring prediction quality, used for cross-entropy loss during both training and evaluation, perplexity calculations, and other language modeling metrics.
4. So What?: Physics-Inspired Open Questions
The following research directions reflect physics-informed perspectives and open questions that I have developed during my exploration; while they may overlap with prior work, I believe they highlight useful angles for further investigation.
Potential Research Directions
Group Theory for Neural Circuits
Could we apply group theory (successfully used to organize the "particle zoo" in the 1950s-60s) to systematically group neural circuit patterns for better interpretability? Just as group theory revealed underlying symmetries that organized seemingly random hadrons into the Eightfold Way and eventually led to the quark model, similar mathematical frameworks might help classify the multitude of neural network pathways and patterns.
Many-Body Neural Systems
While we understand individual neurons, understanding group behavior remains elusive - reminiscent of the reductionist vs. holistic challenge in physics. Statistical mechanics deals with many-body systems and macroscopic properties. Could these approaches better explain neural network behavior than trying to understand individual components?
Scaling Laws Meet Phase Transitions
The sharp, discontinuous emergence of new abilities at critical model scales resembles phase transitions in physics, where smooth parameter changes trigger sudden qualitative shifts. This apparent paradox with smooth scaling laws mirrors how underlying variables (like temperature) change gradually while observable properties (like magnetization) change abruptly at critical points. Could identifying the neural equivalents of critical mass phenomena help predict emergence thresholds, or do we need frameworks that unify both gradual scaling improvements and sharp qualitative transitions in AI systems?
Methodological Questions
Measurement-Driven Discovery
I've learned that many breakthroughs in brain science emerged from defining precise measurable quantities. Karl Friston's free energy principle exemplifies this pattern—by mathematically defining free energy as an information-theoretic quantity, he unified previously separate theories under one measurable framework [4]. Similarly, Geoffrey Hinton's work at University of Toronto applied Boltzmann distributions from statistical mechanics to create breakthrough AI architectures, recently recognized with the 2024 Nobel Prize in Physics [5]. This pattern suggests we should think more systematically about what transformative measurable quantities might be waiting to be defined in AI interpretability research.
Measurement Strategy
Also, from an experimental physicist's perspective, what we measure is critical. While cross-entropy loss is optimized for training, is it actually the best way to understand model behavior? Should we measure raw token probabilities, perplexity, or calibration metrics instead of loss? Beyond probability measures, should we also focus on attention patterns, activation magnitudes, or gradient flows? How do we systematically measure emergent behavior with scaling? With so many measurable variables, how can we efficiently extract the high-level patterns that capture the most meaningful information?
Bayesian Approaches to Interpretability
Physics emphasizes precise measurements with quantified uncertainties, while industry ML often defaults to deterministic outputs. Given that the human brain operates as a Bayesian inference engine—continuously updating beliefs from limited evidence—should interpretability research embrace more explicitly Bayesian frameworks? This could be particularly valuable for understanding how transformers handle infrequent but critical decisions where we can't gather sufficient statistics, similar to how humans make consequential life choices without the luxury of controlled trials.
Fundamental Puzzles
Grounded vs. Abstract Meaning
Neural networks feel more mathematical than physical - in physics, information has specific meaning (e.g., particle spin states in wave functions correspond to measurable angular momentum), but in ML, any numerical representation is valid as long as it's useful for the task. Does certain neuron firing patterns have inherent meaning? This fundamental question about the nature of representation needs addressing.
In-Context Learning
How does transformer in-context learning compare to human rapid adaptation? The ability to change behavior without parameter updates seems more like pattern recognition than true learning—what can brain science tell us about this distinction?
Thoughts Under Fermentation
Residual Stream Design Choice
The linear additivity of residual streams makes interpretability possible. This seems to be a good choice, but I wonder if there are any other structural ways to allow interpretability more easily with different design setups.
Appendix
[As of 2025-08-17, this section is incomplete. Needs to be updated.]
References
- 지식 인사이드. "20대로 돌아가면 이것부터 읽을 겁니다." 뇌과학으로 입증된 최고의 책 1권 (박문호 박사 1부). YouTube. https://www.youtube.com/watch?v=79crR-kUGrI
- Coyle, Daniel. The Talent Code: Greatness Isn't Born. It's Grown. Here's How. Bantam, 2009.
- Radford, A., Wu, J., Child, R., Luan, D., Amodei, D., & Sutskever, I. (2019). Language Models are Unsupervised Multitask Learners. OpenAI. PDF
- Friston, K. (2010). The free-energy principle: a unified brain theory? Nature Reviews Neuroscience, 11(2), 127-138.
- The Nobel Prize in Physics 2024. NobelPrize.org. Press Release
- Casali, A. G., et al. (2013). A theoretically based index of consciousness independent of sensory processing and behavior. Science Translational Medicine, 5(198), 198ra105.
- Tononi, G. (2008). Integrated information theory. Scholarpedia, 3(3), 4164.